Text

(pre-publication version, December 26 2011)

IMAGINING A THEORY OF EVERYTHING FOR ADAPTIVE SYSTEMS

        BY  STEPHEN P. COOK

       1.  Introduction: Worldviews, Reality, and a Theory of Everything

  By worldview, I mean the conceptual framework, beliefs and values used to make sense of reality.  Well-developed worldviews incorporate a cosmology that answers questions like "How did I get here?" or a more teleological "Why am I here?"  To aid analysis and guide worldview development, I have formulated eighty worldview themes  (Cook 2009).  To illustrate their use I interpret something physicist Leonard Susskind wrote, "Modern cosmology really began with Darwin and Wallace.  Unlike anyone before them, they provided explanations of our existence that completely rejected supernatural agents" (Susskind 2006).  My interpretation: from a "Secular Humanism" and "Scientific Materialism" perspective, these men used the "Scientific Method" in developing their "Global Vision."  In telling a story, they did so without building it around God, the Creator and Father, that is without  "Monotheism" and "Belief In A Personal God."  They shunned use of "Vitalism," "Mysticism," "Magic," and "Religious Fundamentalism."

     Many scientists define objective reality as independent of mind or worldview by limiting it to events and phenomena that can be recorded by devices.  Reality is  different from how we describe it, like the difference between physical terrain and the map of that terrain.  Biblical passages hint at this difference: in Genesis, "In the beginning God created the heavens and the earth," and in John, "In the beginning was the Word, and the Word was with God, and the Word was God." 

     Some feel that scientific accounts of "In the beginning..." are about to change.  Recently Eric Verlinde has advanced efforts to unify the four fundamental forces as part of a "grand unified theory" (Verlinde 2010).  It seems one of the forces, gravitation, can be understood as something else: "an entropic force caused by changes in the information associated with the positions of material bodies."  Verlinde deduced this using some new physics: the holographic principle.  Perhaps difficulties reconciling the theory of gravity (general relativity) with the wildly successful, but difficult to understand, theory of quantum mechanics are over? 

     We mustn't get our hopes up!  I don't think a "theory of everything" (TOE) is right around the corner.  I don't think we'll ever have a map of reality that perfectly represents the terrain, or a model that gives perfect predictions for everything of interest.  A worthy goal is making them increasingly useful.  Physicist James Hartle, who in 1983 collaborated with Stephen Hawking in a paper entitled "Wave Function of the Universe," tells a story about Murray Gell-Mann (Hartle 2003).  Murray used to ask Hartle, "If you know the wave function of the universe, why aren't you rich?"

     Certainly seeking fundamental understanding is important and there is more to life than economic gain.  But environmental concerns point to problems scientists might work on that seem especially urgent.  In this paper I imagine what might inspire the construction of a useful TOE, then consider how it might be formulated.  I begin by identifying what questions such a theory should attempt to answer.  At the top of my list I'd put a problem, "How can humans adapt and learn to live as part of nature?"  Solving that might require exploring "Who are we?" and "How'd we get here?"   

     Daniel Dennett describes Darwin's Dangerous Idea as the notion that design can emerge in the natural world from mere order via an algorithmic process, rather than requiring an intelligent creator (Dennett 1995).  Skeptics see it as highly improbable that blind, mindless, random processes could have produced seemingly purposefully designed complex structures.  Richard Dawkins answers them in Climbing Mount Improbable with an analogy emphasizing the power of accumulation (Dawkins 2004).  "On the summit sits a complex device such as an eye or a bacterial flagellar motor.  The absurd notion that such complexity could spontaneously self-assemble is symbolized by leaping from the foot of the cliff to the top in one bound.  Evolution, by contrast, goes around the back of the mountain and creeps up the gentle slope to the summit--easy!"

     While biologists overwhelmingly accept Darwin's idea, other scientists including physicists and cosmologists are not so sure.  As Susskind describes it, "The bitterness and rancor of the controversy have crystallized around a single phrase--the Anthropic Principle--a hypothetical principle that says that the world is fine-tuned so that we can be here to observe it!"  In The Cosmic Landscape, he describes "the illusion of intelligent design" and provides a "scientific explanation of the apparent benevolence of the universe," one he calls "the physicist's Darwinism."  He believes an eternal inflation mechanism has created a "bubble bath universe."  Space cloning itself in nucleating bubbles has conceivably produced 10⁵⁰⁰ possible separate universes.  While not all of these actually exist, enough do to make our part of this megaverse look like nothing special.   While it's obviously compatible with the intelligent life we represent, most other pocket universes are not.  Susskind thinks maybe we're just lucky after all!

     Clearly any TOE needs to once and for all answer the question, "How, why (if there is a reason), and when was the universe created?"  For those still clinging to an Intelligent Designer, if a TOE posits one, it must address questions like, "How did the Intelligent Designer come into being?" and "What maintenance (if any) on this design does the Intelligent Designer do?"

     Surviving in nature requires building and continually refining an internal model of it--something which requires constant "dialogue with nature" to use Prigogine's phrase (Prigogine 1997). "What makes this dialogue possible?" he asks.  In arguing time is real and connected with irreversible processes, he responds, "A time reversible world would also be an unknowable world. There is an interaction between the knower and the known, and this interaction creates a difference between past and future."  Those who believe time is an illusion would disagree.  We'll want to ask, "What is time?"

     Poet and mystic William Blake imagined it might be possible "to see a world in a grain of sand." Given renewed interest in hologram-like universes, it seems we'd want our TOE to tackle "Does the universe somehow contain its whole essence in every part?"   Some mystics equate the universe with God; others believe a living consciousness pervades the universe, something they equate with the Cosmic Mind, or God.  We'll need to ask, but we're getting ahead of ourselves!  Certainly before we make that inquiry, we've want a full explanation of consciousness and its relationship to life.                  

     Speaking of life, a TOE should describe what forms it exists in throughout the universe and explain its origin.  We'd like detailed instructions on how to make it from non-living building blocks.  Speaking of building blocks, we'd like to know, "Of what fundamental stuff is the universe made?"  Are matter and energy more fundamental than space?  Perhaps information or consciousness or vital spirit is more important still?  And what exactly will happen to that inner essence I think of as myself after my body dies?  It seems our expectations of a TOE are so great there is no end to the questions!  

2.  Building Information Concepts and Optimizing Principles into a TOE  

I could call the fundamental mechanism by which information is exchanged, how "it" becomes "bit," "handshaking" or "pinging."  Instead I'll relate it to action and Newton's Third Law: forces come in pairs: action forces and reaction forces.  Action forces and action, though related, are different.  Action refers to an amount of energy transferred in a process multiplied by the time elapsed Δt.  Optimizing principles are laws in which some physical quantity must be a maximum or minimum under certain conditions.  Action is such a quantity; entropy, a measure of disorder, is one; free energy is another. 

     The second law of thermodynamics says the entropy of an isolated system can only remain constant or increase, the latter occurring where irreversible processes are involved.  Life's processes, in tending toward increasing organization and decreased entropy, seemingly violate this law, but that's only because they are open systems.  For a larger system made up of living creature and surrounding environment, the decrease in entropy in the living subsystem is offset by increased entropy in the environment.  

     While the second law can be seen as a principle of maximum entropy, it can also be connected to energy transfer and gradients.  In this form it prohibits a spontaneous transfer of heat from lower to higher temperature regions.  By itself, heat doesn't move up the "temperature hill."  In general, one can view nature's inexorably driving matter toward equilibrium as pushing it downhill toward stability, and attempting to level any gradients that exist in the process.  As Eric Schneider puts it, "Nature abhors gradients" (Schneider 2004).

     In creating order and existing far from equilibrium, life seemingly resists nature's leveling tendencies--but only if one focuses on living system S.  Schneider believes that detailed energy accounting for both S and surrounding environment E, shows that life represents a particularly efficient way of carrying out nature's overall increasing entropy, leveling, and seeking equilibrium mandate.  For inanimate matter, Verlinde's connecting forces with entropy gradients, wonderfully illustrates this.  He traces the origin of gravity and inertia to nature's seeking to maximize entropy.  Appreciating his argument requires understanding entropy from an information theory perspective.

     Inspired by Boltzmann's 1877 characterization of entropy in terms of the number of possible microstates which are available for a macroscopic system to occupy, in 1948 Claude Shannon conceived of measuring information content in terms of binary digits (bits) needed to describe it.  While convention specifies thermodynamic entropy and Shannon's information related entropy in different units, when calculated for the same number of possible microstates or degrees of freedom, they are equivalent.

     Information is not just an abstraction, it has a real representation, being encoded in atomic or molecular energy levels, spin states, sequences of nucleotide bases, neural synaptic connection patterns, etc.  Rather than information quantity, information transfer deserves attention.  As Bateson pointed out, "All receipt of information is necessarily the receipt of news of difference" (Bateson 1979). 

Physicists connect information transfer with energy and entropy transfers.  Suppose an electron's spin changes from up to down.  Not only is there an energy transfer associated with that event, communicating the knowledge requires energy to successfully transmit it through a background of noise.

     Entropy changes as information is transferred.  Whereas a system in thermal equilibrium with the environment has maximum entropy, its randomness suggests maximum uncertainty and algorithmic incompressibility.  There is no discernable message for an observer trying to extract a signal carrying information from such a source.  Generally speaking, the entropy of a system has decreased if its state after the event (measurement, information transfer, etc.) is more sharply defined (less uncertain) than before, and the entropy of the surrounding environment has increased.   Where life is concerned, living systems have been described as "sucking information out of the environment," and their fitness determined by "the most fit is the best informed."  Such systems pull energy from the environment and occupy low entropy, minimum uncertainty states. 

    Whereas entropy is often associated with unorganized or useless energy, free energy is connected with energy capable of doing useful work.  Like entropy, free energy has been interpreted in an information theory context.  Karl Friston, a neuroscientist, has examined theories about how the brain works (Friston 2010).  He writes, "if we look closely at what is being optimized, the same quantity keeps emerging namely value (expected reward, expected utility) or its complement, surprise (prediction error, expected cost).  This is the quantity that is optimized under the free energy principle."

     Friston's free energy gauges some difference of interest between living system and environment. Grandpierre has used extropic energy in making a similar assessment  (Grandpierre 2007).  Verlinde's conception of gravity is based on equating an energy difference, between a configuration of matter and an equilibrium configuration, with both work done by a restoring force and the product of temperature and change in entropy. 

     Depending on the interpretation, free energy, extropic energy, entropic energy, traditional Lagrangian, or combinations of these are appropriate as "energy difference" input to action principles.  Such principles can be generalized and made more applicable.  In this regard consider a generalized optimal action principle (GOAP) that maximizes stability:

                  δ (generalized action) = δ  ( ∫ (energy difference) dt ) = 0                   (1)

Here variation δ requires generalized action be optimized, minimized or maximized, over some path in some unspecified (real, phase, or conceptional) space. 

     Applying the GOAP requires computing generalized action.  Imagine system S changes state, moving along some path from point 1 at time t₁ to point 2 at time t₂.  Computing the generalized action involves breaking the path up into tiny time intervals, multiplying the energy difference for each one by the tiny time duration, and summing (integrating) these products over the path.  If S is non-living, the energy difference can be the total energy (the Hamiltonian) minus the potential energy that exists between system and environment stored in the conservative force field.  For living system S, the energy difference can be interpreted in different ways. Whether generalized action is minimized or maximized depends on the system being considered. 

     If boundaries are drawn to solely include a living system, summing up the products of energy transferred from the environment by time over a path representing the lifetime of the system will maximize generalized action.  If system boundaries are drawn to include the surrounding environment, generalized action is minimized.  Entropy is maximized, but in attaining equilibrium the associated energy difference between the matter part of the system and the environment fluctuates around zero.  Many will argue that for living systems in a steady state (homeostasis), generalized action will be only locally minimized since the path will not include the death of the organism (where it arrives at a true minimum).  Schneider disagrees.  He believes life represents the most efficient way to degrade energy.  His models suggest life's processes maximize entropy faster than a system that did not include living creatures would  (Schneider and Kay 1994).

     Complex adaptive systems (CAS) that learn from their environment can be considered as minimizing generalized action.  This is accomplished by a system that represents an internal model the CAS has of itself and of the environment.  Ideally the fit between system and environment is an increasingly good one over time.  I view Friston's free energy principle, based on his modeling of the brain, as calculating generalized action based on (what he calls) surprise or a quantity gauging system minus environment prediction error expressed in information theory terms.  Then, minimal generalized action means minimal uncertainty, meaning the most probable, most stable state. 

     In concentrating on the interaction or fit between system and environment, the GOAP recognizes "physics is simple only when analyzed locally" (Misner 1973).  Information transfer requires the hand-shaking of action/reaction force pairs. We interpret Newton's Third Law to mean "if the system pushes on the environment, the environment unavoidably and instantaneously pushes back on the system." 

  3.  Building Adaptive Mechanisms into a TOE

 The GOAP applied to living systems can quantitatively assess life adapting to its environment.   What specific adaptive mechanisms are employed?  Classically, we think of genes experiencing mutations (changing genotype) and expressing themselves (changed phenotype) in the structure or behavior of the organism.  Mutations that enhance survivability and lead to more copies eventually establish themselves within the population.  Such changes are called adaptations.  In this way, the fit between an organism and its environment improves.  This fit can vary due to environmental changes, forcing whole populations to respond by adapting or dying out.  Mutations and resulting adaptations are usually thought of as part of  a slow process, like a drunk setting off from a street corner in random walk fashion.  As we shall see, quantum random walks may speed up this process. 

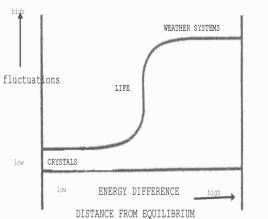
     Complex adaptive systems (CAS) can speed up the learning about the environment process.  Where such a system is positioned in a 3D fitness landscape determines what adaptations it can make.  Before considering such a plot, note where life is found in a simpler diagram (Fig. 1): at a medium distance from equilibrium where structures experience a range of fluctuations, where maximum capacity for adaptability lies (Macklem 2008).  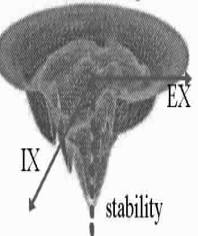To further distinguish living CAS from non-living systems, consider Fig. 2, where stability  (the inverse of biologists' fitness function) is plotted vertically down from a 2D horizontal plane.  There, potential niches are identified using two variables (expressed in energy units): a system's distance EX from thermodynamic equilibrium, and the amount of information IX it exchanges with the environment. 

            Fig. 1   Life at the Edge of Chaos            Fig. 2  Fitness Stability Landscape

 

     In this plot, the deeper the valley, the greater the stability, and the steeper the slope, the greater the selection pressure.  It pictures the stability the GOAP could conceivably specify mathematically for complex systems.  For a CAS, the worst place to be is at the origin, where EX=0 and IX=0, representing equilibrium (death).  The randomness here represents maximum uncertainty in terms of trying

to extract a message, meaning information transfer between system and environment is impossible.  The best place is in one of the not so deep valleys a medium energy distance away from the origin and "on the edge of chaos."  Langton says this is where "information gets its foot in the door in the physical world, where it gets the upper hand over energy" (Lewin 1992).                             

     A diversity of living systems--ecosystems, immune systems, neural networks, and genetic landscapes--have been successfully modeled using both simple binary networks and more advanced networks known as cellular automata.  One such model is the Game of Life, invented in 1970 but recently in the news with a discovery that prompted this headline: "The Life Simulator--a self replicating creature that might tell us something about our own beginnings" (Aron 2010).

     Before life's origin can be nailed down, we need to agree on a definition of it.  By 1950 von Neumann decided living things differ from machines in that, unlike machines, they not only reproduce themselves, but also do self-repair.  Biologists' definitions typically included homeostasis, meaning systems work together to maintain the internal temperature, pressure, nutrient levels, waste products, etc. within normal ranges.  The new field of cybernetics helped to broaden the conception of life.  Norbert Wiener was fascinated by systems where "causes produce effects that are necessary for their own causation" (Wiener, 1948).  With understanding of DNA and messenger RNA, it soon became apparent that a nice closure existed in the genetic code and its operation: "nucleotides code for proteins which in turn code for nucleotides" (Prigogine 1997). 

     By the mid 1970s, Varela and Maturna had described the organization typical of most adaptive systems (Varela 1974).  Using the term autopoietic system, they characterized it in similar circular fashion, noting "the product of its operation is its own organization."  Besides this conceptual closure, they recognized the importance of a boundary (cell membrane, etc.) that provided physical closure.  To them, living things are built around three interwoven things: an autopoietic pattern of organization, embodied in a so-called dissipative structure, and involved in a structural coupling life process they call cognition.  Acts of cognition, they say, produce structural changes in the system, which itself specifies which perturbations from the environment trigger such changes.  Just as Prigogine, whose dissipative structures concept they borrowed, liked to stress the dynamic, spontaneous aspect of life by emphasizing its "becoming" rather than its "being," Maturna and Varela, felt "to live is to know." 

     Stuart Kauffman has investigated NK genetic fitness landscapes.  Learning from complex binary network models with N nodes and K inputs to each node, he located the boundary between order and chaos in the K=2 region.  Below that periodic attractors became, as K decreased, more stable point attractors.  As K steadily increased above 2 strange attractors and totally chaotic behavior resulted.  Using a more sophisticated model and random adaptive walks, Kauffman let the genes of different organisms interact and found the evolving genes of one organism altering the fitness landscape of other organisms.  He eventually concluded, in the words of science writer Roger Lewin, "coevolving systems working as CAS tune themselves to the point of maximum computational ability, maximum fitness, maximum evolvability" (Lewin 1992).

     In an effort to improve their fit with the environment, some CAS have a mechanism for anticipation, based on pattern seeking and internal models of the environment.  According to Holland, these take two forms, tacit and overt (Holland 1995).  The first "simply prescribes a current action, under an implicit prediction of some desired future state."  He cites "a bacterium [moving] in the direction of a chemical gradient, implicitly predicting that food lies in that direction."  In contrast, more advanced CAS use both tacit and overt models. The latter "is used as a basis for explicit, but internal, explorations of alternatives, a process often called look ahead."  The internal model physically realized in neural network connections in our brains is often employed for this purpose.

     Some CAS maintain a dialogue with nature in which feedback continually informs internal models by testing the predictions they make with real experience outcomes.  According to Friston, the human brain employs Bayesian probability to continually update probabilities of certain outcomes based on new information  (Friston 2010). Unlike most complex systems, human internal models include not only system and effect of the environment on the system, but also effect of the system on the environment.  It seems that neither top down or bottom up one-way processes are typically found in nature's mechanisms, instead circular feedback loops are everywhere. 

     Dennett has characterized evolution over geological time in terms of matter steadily relying less on random dumb luck and more on skill (Dennett 1995).  This skill, in the form of pattern recognition programs sorting and winnowing to gather information, storing it in structures that grow in complexity over time, learning about the environment through feedback, has been slowly acquired.  Systems able to take advantage of a fortunate position in a fitness landscape learn faster and adapt better than others. Natural selection weeds out those that don't.  In the long run, not just individual organisms, but whole ecosystems evolve in a way that maximizes fitness and stability. 

 4.  Building Understanding of Mysterious Information Transfer into a TOE            

 Consider mysteries involving living creatures.  By some accounts, green plants convert sunlight into chemical energy with nearly 100% efficiency; birds find their way back to preferred sites after journeys of thousands of miles; after intercourse, humans are naturally drugged and their lethargic inactivity gives sperm a better change of fertilizing an ovum. 

     To physicists used to thinking about forces causing certain effects, these are troubling examples of life directing its future behavior, of processes where goals seemingly initiated at higher levels in a system's organizational hierarchy dictate what happens at lower levels.  They seemingly involve teleology and downward causation mechanisms.   They are difficult to explain.  Perhaps the ultimate mystery for evolution to explain is consciousness, described as an emergent phenomenon in a multi-leveled system in our brain where "the top level reaches back down towards the bottom level and influences it" (Hofstadter 1979). 

     The mysteries aren't confined to the living world--the quantum world is full of them.  Consider something as simple as the famous double slit experiment of physics, in which light shines on a screen containing two narrow slits.  Which slit do individual photons go through in producing the interference pattern seen on a second screen?  It seems like they go through both of them simultaneously and they are both particles and waves!  Many feel understanding this is the key to making sense of quantum mechanics and explaining many of life's mysteries. 

     Before applying the GOAP to quantum systems, consider one statistical physics approach to handling systems involving large numbers of interacting particles.  This can involve isolating each particle S_i of the system and studying its Brownian motion.  In the resulting random walk, each step, due to a collision with a particle E_j in the environment, would be expected to cover distance d₁₂= the square root of N, where N=# of collisions or steps between times t₁ and t₂.  (Feynman 1963)

     An optimal action principle is used in quantum mechanics, with the action appearing in the phase of wave functions.  Feynman's path integral formulation (Feynman 1965) supposedly removes teleological concerns about how the particle knows the "right" path to take.  It involves calculating the probability of the particle taking a particular path, and doing this for all possible paths.  The process can be connected to quantum random walks, which have significant advantages over classical random walks.  They are more efficient at moving particles: particle S_i taking N steps between times t₁ and t₂ would be expected to travel distance d₁₂=N, quadratically faster (Kempe 2003)! 

     Quantum random walks seemingly allow systems to do something analogous to what a good chess player does: analyze all possible moves and pick out the best one before it is made.   Perhaps this can explain what puzzled physicist Roger Penrose back in 1989, when he said,  "There seems to be something about the way the laws of physics work which allows natural selection to be a much more effective process than it would be with just arbitrary laws" (Penrose 1989).  How do the laws of physics explain this and other mysteries of the quantum world?

    In the last three decades, physicists in the tradition of Bohr and Wheeler, have made progress in understanding how particles like photons choose a particular path and how classical trajectories emerge from the randomness of the quantum world.  One of their leading theories is Quantum Darwinism (Zurek 2003).  It uses an Environment Induced Selection rule, based on minimizing uncertainty, to explain which of a multitude of possible quantum system states are actually physically realized.  These quantum states, which actually survive to have more than an imagined, virtual existence, are called pointer states.  The extent to which these states disseminate and are redundant measures their fitness.  Using GOAP, and thinking of a ball naturally rolling to a stable, lowest energy position of equilibrium in a gravitational field, I see pointer states as follows.  Of many possible systems operating between fixed points between times t₁ and t₂, they represent those in which the generalized action, based on the energy difference between them and the surrounding environment, is minimal--meaning they are the most stable states. 

     Why is this called Quantum Darwinism?   I think of a Darwinian process as follows. Copies, some slightly different, are made of the original initial system S; these copies' fit with their environment varies; as time passes, and natural selection does its work, the population of copies of S will reflect the fitness (i.e. the most fit copies will survive and produce more copies).  Respecting a (no-cloning) theorem that forbids making copies of pure quantum states, in Quantum Darwinism the most robust, most stable pointer states replicate the most in the classical realm.  These interact with the environment, leading to slight variations of them, and the testing by natural selection you'd expect.       

     In general, the quantum state of the system is a superposition of many individual states.  The coupling or coherence that exists between two of these individual states can be likened to the interference effects seen between light waves emanating from the two slits in the double slit experiment.  Just as forcing a photon through one slit or the other by measuring its position destroys the interference effects, measurements or interaction with the environment destroys coherence in quantum systems.  While Quantum Darwinism details how information about decohering systems is coded in the environment, quantum  computing involves working with (initially) coherent quantum systems to encode information and avoiding decoherence.  So each step of a quantum random walk is made without an intermediate measurement, which would destroy information and its advantage over its classical counterpart.  A quantum walk can be seen as a process in which a system learns about its environment without provoking it. 

     Nature apparently employs quantum random walks, most notably in its design of a key photosynthetic mechanism as the following news item highlights.      "Photosynthetic proteins are 'wired' together by quantum coherence for more efficient light harvesting in cryptophyte marine algae" says a report in Nature (Collini 2010).  It's referred to as nature's "quantum design for a light trap."  Seemingly the photons involved explore all possible paths and pick the best one.  The previous week another group reported finding unexpected long-lived quantum coherence at room temperature in photosynthetic bacteria. (Engel 2010)  They cite protection provided by a "protein matrix encapsulating the chromophores," and assert "the protein shapes the energy landscape and mediates an efficient energy transfer despite thermal fluctuations."

     How photons know the best path to take is one mystery physicists seek to explain using quantum theory, another involves how the hundred or more amino acids in proteins so quickly fold into the correct shape to become biologically active.  After a stunning breakthrough in modeling why such folding depends on temperature in such an unexpected way (Luo 2011), it seems clear that a quantum approach is needed to understand this mystery. A third mystery involves resolving the incompatibility between quantum field theories, one being quantum electrodynamics in which the photon serves as field particle, and the holographic principle. Basically field theories allow an infinite number of degrees of freedom, whereas holography restricts these to a finite number.  According to the latter, our universe has two alternate, but equivalent descriptions (Bousso 2002).  One is provided by information that fills the 3D (or ND) volume of space, the other by information stored on a 2D ([N-1] D) surface bounding the volume.  The descriptions are equivalent, so the maximum amount of information that can be stored in a region, or equivalently its entropy, depends on its surface area, not volume.  Could it be the universe acts like a giant hologram with information transfer being the fundamental process?

     Like holography, certain quantum phenomena suggest the possibility of non-local information transfer.  From experimental tests of Bell's theorem, physicists  conclude that for two coherent, entangled particles, what happens at one place to one of them can instantaneously affect the other, no matter what distance separates them (Kuttner 2010).  Could it be in this virtual world of entangled photons, time does not exist?  A TOE could clear up many mysteries involving information transfer, whether they arise from seeming downward causation, quantum weirdness, etc.  A final one that deserves mention: how random matrix theory, developed to model quantum fluctuations but increasingly applied to diverse phenomena, hints at a "deeper law of nature" (Buchanan 2010).  

5.   Building Mechanisms for Improving Conceptual Models into a TOE      

The conceptualization process involves observing, abstracting, recalling memories, discriminating, categorizing, etc.  As you grow, you steadily organize these concepts into conceptual schemes, and put those schemes into a framework.  Gabora and Aerts seek to explain this worldview development process using a model and a theory of concepts, known as SCOP, for State COntext Property (Gabora and Aerts 2009).  They consider "how concepts undergo a change of state when acted upon by a context, and how they combine."  After building a formalism that begins with a set of states the concept can assume, and another set of relevant contexts, they identify a theoretically possible (but in practice difficult to observe) "ground state" of a concept as "the state of being not disturbed at all by the context."   A context "may consist of a perceived stimulus or component(s) of the environment...or entirely of elements of the associative memory."    

     They add concept states together like a linear superposition of quantum states, identify a "potentiality state...subject to change under the influence of a particular context," and liken the change of state associated with this to quantum state collapse.  I see their concept states as system states, and context states as the environment.  They go on to define a cognitive state in an individual's mind as "a state of the composition of all of [the] concepts and combinations of concepts of the worldview of this individual," discuss how they employ SCOP to study how "more elaborate conceptual integration" can be achieved, and proclaim the worldview is "the basic unit of evolution in culture." 

     I like the thought of competing worldviews.  Seems to me the competition will be decided on the basis of which model best represents reality as measured by the ability to make useful predictions over the time frame of interest.  And how well the conceptional system representation S fits the real environment representation E.  The winner will be the worldview that minimizes the S-E difference over the relevant path in conceptual space.  Perhaps a next step is translating that difference into energy, or prediction error information counterpart, and applying the GOAP!  

6.  Putting it All Together

 Here's a recipe for using my imagined TOE to attack certain problems of interest. 

1) Define the problem, gather data, define system and hierarchy.   Quantify system <===> environment relationship and build initial model.  Identify and attempt to quantify, uncertainties and approximations.  If modeling a system that learns from the environment like a CAS, provide an internal model and provide for Bayesian updating.   Build in and quantify adaptive mechanisms, feedback loops, autopoietic organization.

2) This model will use the GOAP to optimize fit between system and environment.

3) Refine the model by testing using related problems with known solutions.

4) Construct initial candidate (imagined optimum system) to use as input.  Create more by making slight alterations, combinations.  Test using Darwinian selection.

5) Let output dictate what steps need repeating, perhaps for another part of system.

6) After many iterations, after runs for various subsystems if need be, the model's output should converge on an optimum solution, specifying how well the selected system adapts to the environment, gauged by reproductive, perpetuative, or predictive success over time.

7) How fast steps 4)--6) above are carried out may depend on how (or if) the model and the TOE use quantum techniques (quantum computing, accessing virtual information, etc.).

     At its core is optimization based on the Generalized Optimal Action Principle (GOAP) and use of Darwinian natural selection.  Given the amazing range over which these techniques are potentially applicable, we might refer to the latter as Universal Darwinism!  Conceivably, it might be applied to quantum states (Quantum Darwinism), genes (biological evolution), neural networks (brain), conceptual frameworks (worldviews) or universes.  For the latter, Susskind cautions the cosmological natural selection he describes doesn't involve competition among pocket universes for resources.  For social problems, this recipe may not help--see "Dancing With Systems" (Cook 2009)!

7.  References 

Aron, J. (2010) "The Life Simulator" in New Scientist, 19 June 2010

Bateson, G. (1979) Mind and Nature: A Necessary Unity  Dutton, New York, USA

Bousso, R. (2002) "The Holographic Principle" in Reviews of Modern Physics, 74: 825-874

Buchanan, M. (2010) "Random Matrix Theory" in New Scientist, 10 April 2010

Collini, E. etal. (2010) "Coherently Wired Light-harvesting in Photosynthetic Marine Algae at Ambient

     Temperature" in Nature 463:  644-47

Cook, S. (2009)  The Worldview Literacy Book   Parthenon Books, Weed, NM USA

Dawkins, R. (1996) Climbing Mount Improbable  Norton, New York, USA

Dennett, D. (1995) Darwin's Dangerous Idea  Simon & Schuster Publishers,  New York, USA

Engel, G. etal. (2010) "Long-lived Quantum Coherence in Photosynthetic Complexes at Physiological

     Temperature" arXiv:1001.5108v1 [physics.bio-ph]

Feynman, R. (1963) Lectures in Physics, Vol. 1  Addison Wesley, Reading, MA USA

Feynman, R. , Hibbs, A. (1965) Quantum Mechanics and Path Integrals  McGraw Hill, New York

Friston, K. (2010) "The Free Energy Principle: A Unified Brain Theory?" in Nature Reviews Neuroscience  advance online publication 13 Jan 2010

Gabora, L,  Aerts, D. "A Model of the Emergence and Evolution of Integrated Worldviews" Journal of

     Mathematical Psychology 53: 434-451

Grandpierre, A. (2007) "Biological Extension of the Action Principle"  NeuroQuantology, 5: 346-362

Hartle, J. (2003) "Theories of Everything and Hawking's Wave Function of the Universe" in The Future

     of Theoretical Physics and Cosmology  Cambridge University Press, London, UK

Hofstadter, D. Godel, Escher, Bach: an Eternal Golden Braid  Random House, New York 1979

Holland, J. (1995) Hidden Order: How Adaptation Builds Complexity Helix Books, Reading, MA USA

Kempe, J.  (2003) "Quantum Random Walks--An Introductory Overview" Contemporary Physics 44:

     307-327

Kuttner, F. and Rosenblum, B. (2010) "Bell's Theorem" in The Physics Teacher 48: 124-130

Lewin, R. (1992)  Complexity: Life at the Edge of Chaos Macmillan Publishing Co. New York, USA

Luo, L. and Lu, J. (2011) "Temperature Dependence of Protein Folding Deduced from Quantum Transition" arXiv:1102.3748v1 [q-bio.BM]

Macklem, P. (2008) "Emergent Phenomena and the Secrets of Life" in J. Appl. Physiol 104:1844-1846

Misner, C., Thorne, K., and Wheeler, J. (1973) Gravitation  W.H. Freeman, San Francisco, USA

Penrose, R. (1989) The Emperor's New Mind  Oxford University Press, Oxford, UK

Prigogine, I. 1997  The End of Certainty The Free Press, New York, USA

Schneider, E. (2004) “Gaia: Toward a Thermodynamics of Life” in Scientists Debate Gaia,

     ed. Schneider, S. , etal. MIT Press, Cambridge, MA USA

Schneider, E. and Kay, J. (1994) "Life as a Manifestation of the Second Law of Thermodynamics"

     Mathematical and Computer Modeling 19 (# 6-8):  25-48

Susskind, L.  (2006)  The Cosmic Landscape Little,  Brown and Company, New York, USA

Varela, F., Maturna, H,, and Uribe, R. (1974) "Autopoiesis" in BioSystems 5: 187-96

Verlinde, E. (2010) "On the Origin of Gravity and the Laws of Newton" " arXiv:1001.0785v1 [hep-th]

Wiener, N. (1948) Cybernetics  MIT Press Cambridge, MA USA

Zurek, W. (2003) "Decohorence, Einselection, and the Quantum Origins of the Classical" in Reviews of

     Modern Physics 75: 715- 775

Stephen P. Cook, Project Worldview, Weed, NM 88354-0499 USA; scook@projectworldview.org